רוב המידע שמוצג כאן מבוסס על מאמר מאת Elijah Emerson שניתן למצוא כאן
שמעתם פעם על משחקי אסטרטגיה בזמן אמת (RTS)? אני גדלתי על המשחקים האלה. במשחקי RTS, הרעיון הוא שהשחקן צריך לקבל החלטות בזמן אמת, ולהחלטות האלה כמעט תמיד תהיה השפעה גורלית על אופי המשחק. הסיבה שהאסטרטגיה היא "בזמן אמת", היא שאין פה שום מכניקה של תורות. בזמן שאתה מקבל החלטות ומבצע פעולות, היריב שלך עושה את אותו הדבר. לא מחכים לאף אחד, אם לא תחשוב מהר, תישאר מאחור. דוגמאות מפורסמות למשחקים כאלה יהיו: Command & Conquer, Supreme Commander, Starcraft, Age Of Empires ועוד מלא..
בכמעט כל המשחקים האלו, השחקן מנהל צבא של חיילים ממבט עילי. לשחקן יש את האופציה לבחור חיילים באופן נקודתי או גורף, לקבוע לאן הם ילכו, את מה יתקפו, ומתי יחליטו לסגת. קבלת החלטות איכותיות במהירות (וכמות לא קטנה של Multi-Tasking) תוביל כמעט תמיד לניצחון במשחק.

אבל מה הקשר בין אלגוריתמי ניווט למשחקים מהסוג האלה? ולמה אני מדבר דווקא עליהם? הרי משחקים כאלה הם ז'אנר יחסית קטן של עולם הגיימינג…
כנראה שניחשתם שהקשר הוא התזוזה של החיילים. בשביל שנוכל לגרום לחיילים להגיע מנקודה \(A\) לנקודה \(B\), נצטרך אלגוריתם כלשהו שידע לחשב מסלול.

שימו לב שהחיילים מבינים לבד כי עליהם ללכת מסביב על מנת לעלות על הגשר
אוקיי, אז באיזה אלגוריתם נשתמש? אם יש לכם קצת רקע בנושא, כנראה שאתם חושבים על אלגוריתם \(A^\star\) עכשיו. אלגוריתם \(A^\star\) מאפשר לנו למצוא מסלול אופטימלי מנקודה \(A\) לנקודה \(B\).
ממבט ראשון, השימוש של האלגוריתם במשחקים מהסוג הזה נראה מובן מאליו: ברגע שחייל צריך ללכת מנקודה \(A\) לנקודה \(B\), צריך לחשב את המסלול בו הוא ילך. נעשה זאת עבור כל חייל, ויאאלה אפשר ללכת הביתה.
אבל לצערנו כמובן שזה לא המצב.
בשונה מאפליקציית ניווט, בה צריך לחשב מסלול אחד כל כמה זמן, במשחק RTS, אפילו אחד קטן יחסית, אפשר בקלות להגיע למאות שמחושבים כל שנייה.
וזה לא נגמר שם, במשחק מחשב שמדמה כמות גדולה של חיילים צצה מגבלה נוספת: מה נעשה אם חיילים מתנגשים אחד בשני? אם נבחר מצבור חיילים וננחה אותם פשוט ללכת לנקודה כלשהיא עם \(A^\star\), החיילים "יכנסו" אחד לתוך השני. בגלל שכל אחד מנסה להגיע לנקודה במסלול הקצר ביותר, מבלי להתחשב במיקומים של שאר החיילים.
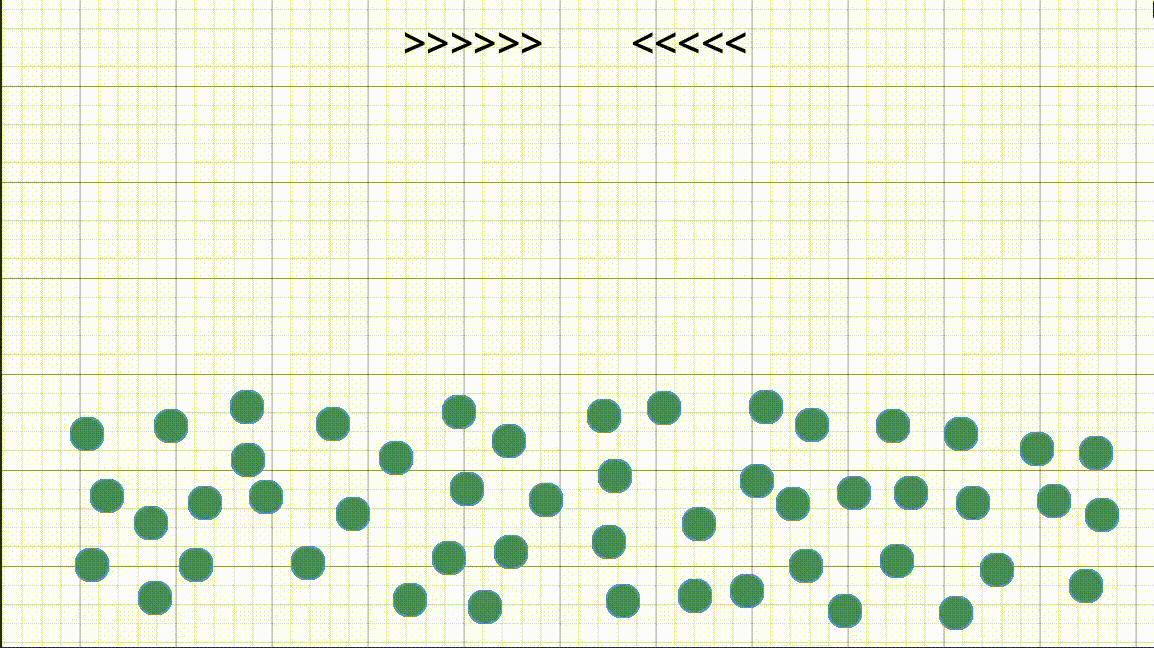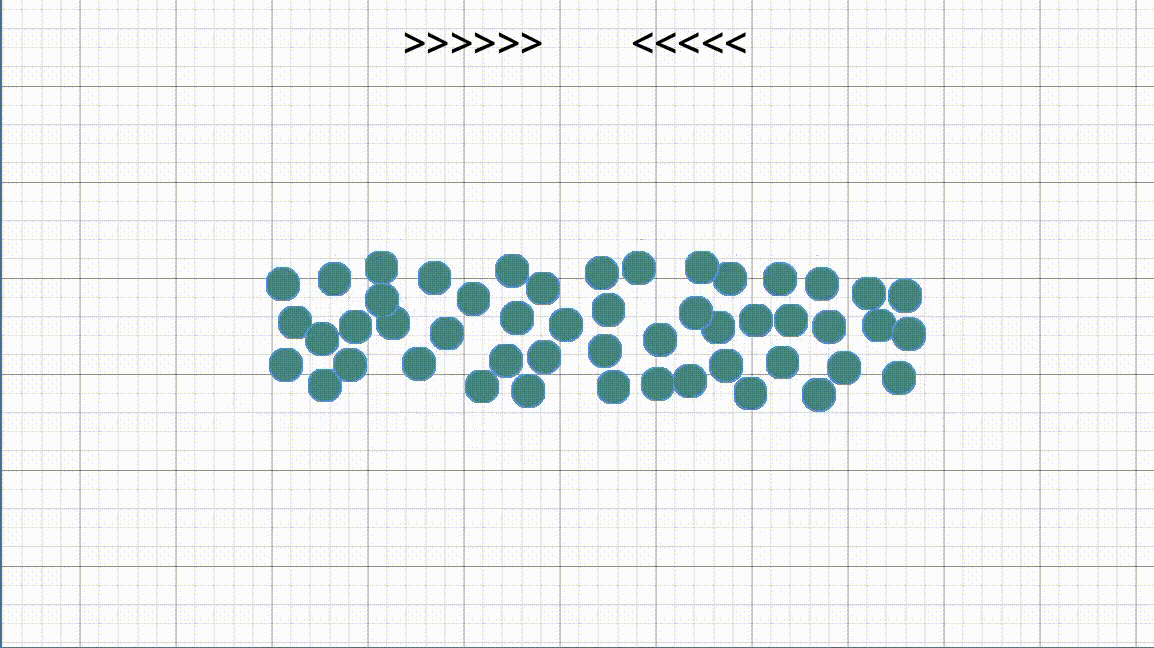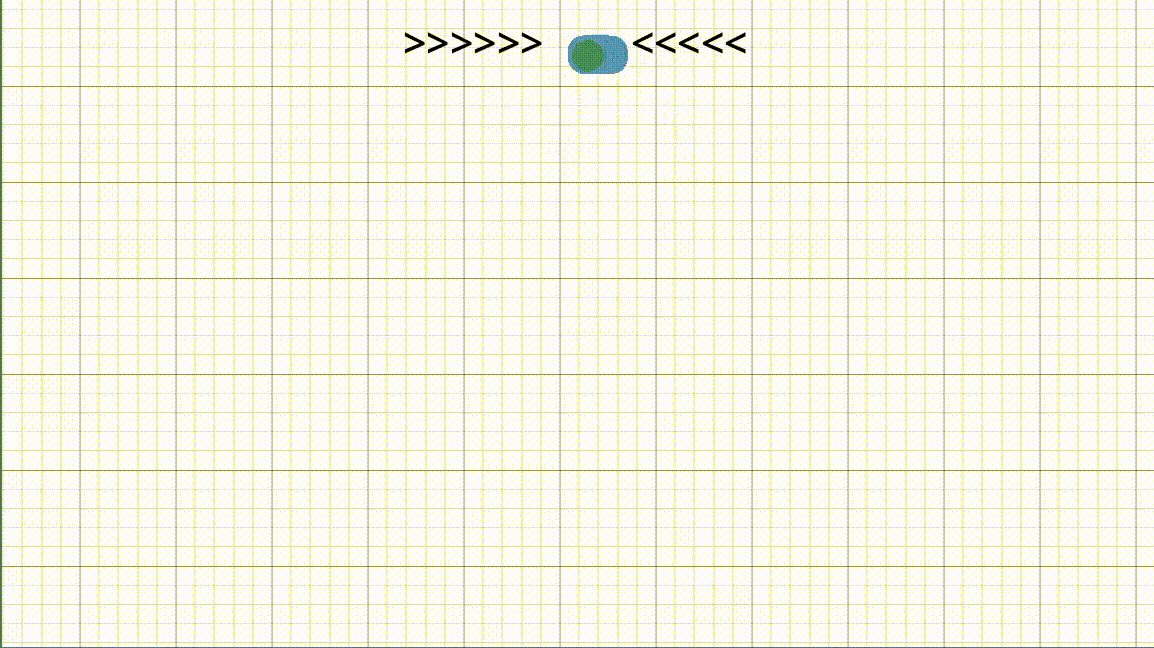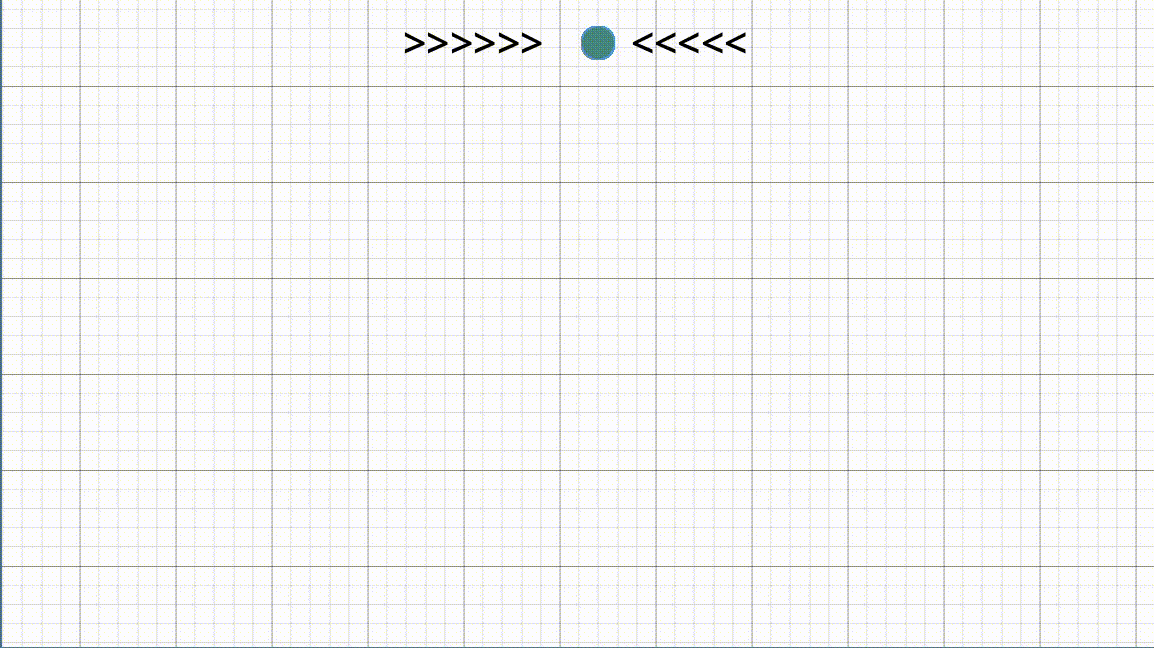
ומהר הבעיה שלנו מסתבכת מאוד. אנחנו עכשיו צריכים לחשב מאות (אם לא אלפים בחלק מהמקרים) של מסלולי \(A^\star\), תוך כדי שאנחנו מתחשבים בהתנגשויות. כלומר במידה וחיילים התנגשו, נצטרך כנראה לחשב את המסלול מחדש.
מיותר לציין שאם ככה נפעל, משחק לא עומד להיות לנו. אלא אם כן אתם מחשיבים מצגת PowerPoint כמשחק.
אז מה אפשר לעשות בשביל לייעל את התהליך?
למזלנו, עולם פיתוח משחקי המחשב מלא במוחות מבריקים עם כישורים יוצאי דופן לבעיות אלגוריתמיות.
בשנת 2010, הושק משחק RTS בשם Supreme Commander 2. המשחק בדומה לרבים כמוהו, עסק בניהול צבא עתידני בזמן אמת. בשונה משאר המשחקים של התקופה, המפתחים של SC2 חשבו על אלגוריתם מעולה על מנת לייעל את הליך חישוב המסלולים. כאן אני אנסה להנגיש כמו שיותר את אופן הפעולה של האלגוריתם הזה, ומה הופך אותו ליעיל היכן שרבים אחרים נכשלו.
בואו נקפוץ ישר לדוגמה חיה.
תסתכלו על המפה שבניתי לצורך הדוגמה (בעורך מפות של משחק מ-2008!):

במפה אנחנו רואים כמה דברים: נהר (ריבועי מאוד, כמו בטבע), עשב, אבנים, ועוד מכשולים על הרצפה, וכמה הרים קטנים.
בואו נסמן 2 נקודות \(A,B\) על המפה הזו ונניח שאנחנו רוצים להגיע מאחת לשנייה:
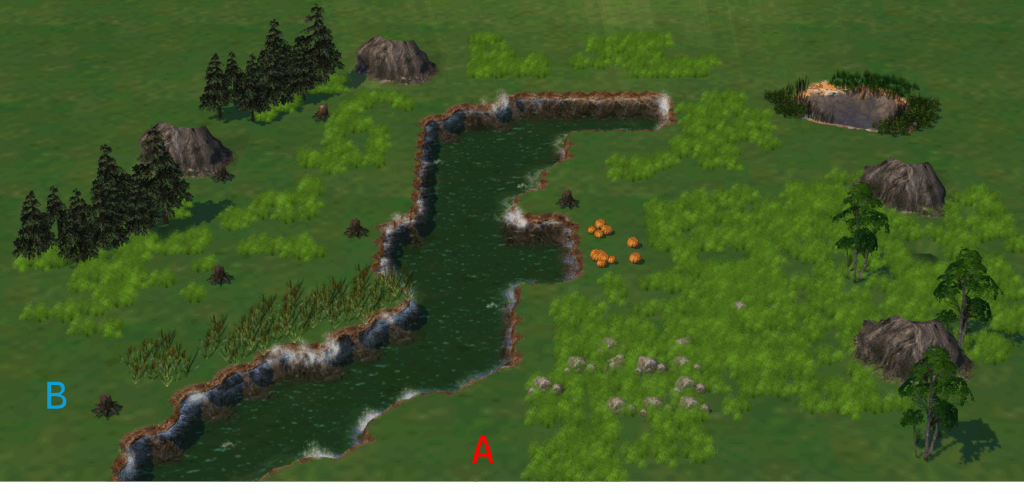
בשביל שנוכל להסביר איך האלגוריתם עובד, נצטרך קודם כל לעבור ממבט תלת מימדי למבט ישיר מלמעלה על המפה. אנחנו גם נחלק את המפה למשבצות כך שכל משבצת היא \(1\times1\) מבחינתנו:

על כל משבצת אנחנו נשמור שלושה שדות מידע שונים. השדות האלה יהיו: מחיר, מחיר מסונן, ושדה זרימה.
לפני שנסביר את שדה המחיר המסונן ושדה הזרימה, בואו נתחיל בפשוט: ערך המחיר של כל משבצת. זה בעצם העלות שצריך לשלם על מנת לעבור דרכה. הערך הזה יאוחסן כ-8 ביטים על כל משבצת (כלומר ערך בין 1 ל- 255), כאשר 255 הינו ערך מיוחד המייצג משבצת שאי אפשר לעבור דרכה. בואו נדגים איך החישוב הזה יראה:
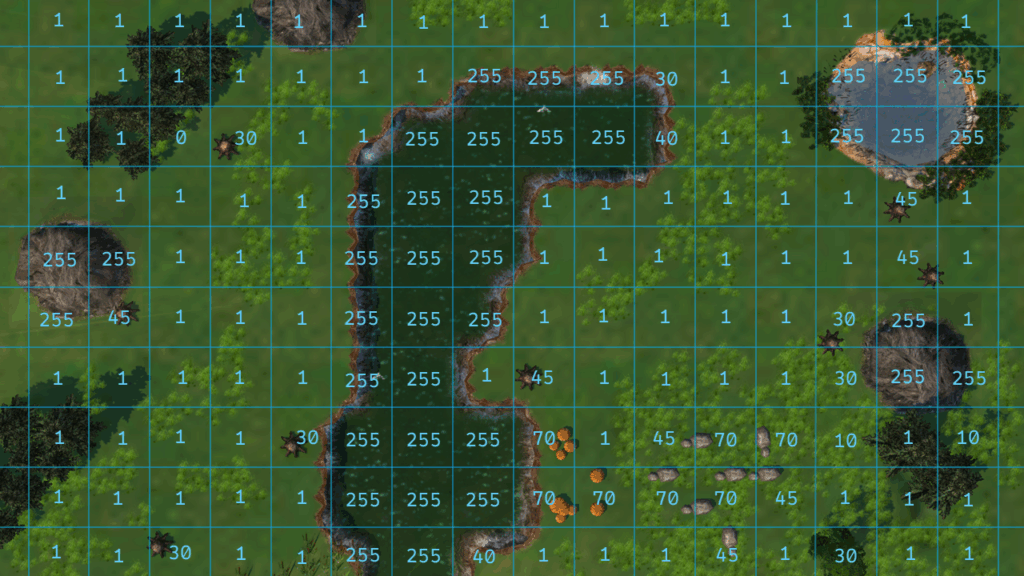
בגלל שהמחיר של כל משבצת לא משתנה במהלך המשחק (אלא אם כן מחליפים מפה), אנחנו יכולים לבצע את החישוב של כל הערכים האלו בזמן טעינת המפה ב-\(O(k)\) כאשר \(k\) הוא מספר המשבצות. עד כה, מאוד פשוט וזול ב-CPU.
בשביל שנוכל להסביר כיצד שני השדות הבאים (זרימה ומחיר מסונן) מחושבים, נצטרך לסבך את הדברים, אבל בהתחלה רק קצת. כרגע אנחנו נשמור את החלוקה למחירים בצד, ונחלק את העולם שלנו לסקטורים. סקטור, זה פשוט מקבץ קבוע של משבצות שאנחנו מחליטים עליו. כאן בגלל שאין הרבה משבצות, בחרתי בסקטורים בגודל של \(4\times3\), אבל לרוב נבחר ב-\(10\times10\). לאחר החלוקה לסקטורים העולם שלנו יראה כך:

מעולה! אבל מה הסיבה לחלוקה הזאת? למה אי אפשר פשוט להסתכל על המפה כמקבץ אחד גדול של משבצות?
תחשבו על זה ככה, נניח ואנחנו מתכננים מסלול אופטימלי במפה שלנו, בכמה סקטורים אתם חושבים שהמסלול יעבור?
בדוגמה שלנו זה אולי קצת פחות ברור, כי באמת סביר שנעבור ברובם, אבל תדמיינו שהמפה הייתה גדולה בהרבה. במצב כזה, כנראה שברוב הסקטורים בכלל לא נעבור, נכון?
בגלל העובדה הזאת, חלוקה לסקטורים תאפשר לנו בהמשך לחשב רק את הערכים שרלוונטים אלינו. כלומר סקטורים בהם אנחנו לא עוברים, מוחרגים מהחישובים.
בשביל שנוכל להשתמש בסקטורים כמו שתיארתי, נצטרך ליצור שערים. תחשבו על שערים כמו על מעברים בין סקטורים. כל משבצת שחולקת גבול עם סקטור אחר, ומותר לעבור דרכה אליו, היא בעצם חלק משער. עוד מעט זה יהיה ברור בהרבה למה זה רלוונטי, אבל לבינתיים בואו נצייר אותם ונוודא שאנחנו מבינים:

שימו לב שכמו שאמרתי, השערים מופיעים רק על גבול דרכו החיילים שלנו יכולים לעבור (החלטה שמתבצעת לפי הערך הכחול על המשבצת, אם הוא 255, לא ניתן).
עכשיו סוף סוף אנחנו מתחילים לנווט. בואו נוסיף קבוצה של חיילים למפה ויעד אליו הם רוצים להגיע:

ועכשיו הקסם של הסקטורים מתחיל: לפני שנתחיל חישובים מסובכים, אנחנו קודם כל נייצר מסלול \(A^\star\) אחד. ליעד שלנו. המטרה של המסלול הזה היא להבין באיזה סקטורים אנחנו כנראה נעבור.

מתחילים להבין את הקטע? אנחנו עכשיו יכולים לסמן את השערים בהם המסלול הראשוני עבר, ובכך להבין אילו סקטורים כנראה לא רלוונטים:

מעולה! הצלחנו לצמצם את הבעיה. עכשיו אנחנו רק צריכים להבין מה החיילים שלנו צריכים לעשות בתוך שמונה הסקטורים הרלוונטים.
הערה קטנה בנוגע למסלול הראשוני
חלקכם אולי שמתם לב למשהו קטן: אנחנו חישבנו מסלול ראשוני מנקודת המבט של חייל אחד מהקבוצה. אבל איך אנחנו יודעים שאותו המסלול אופטימלי עבור השאר? זאת שאלה מעולה. והתשובה היא שאנחנו מחשבים "מסלול ראשוני" דומה עבור שאר החיילים. אבל עבורם אנחנו מבצעים \(A^\star\) מיוחד, שמעדיף לעבור בשערים הסגולים אם זה אפשרי. ככה אנחנו מונעים מצבים בהם השחקן מסמן קבוצה של חיילים, וכשהוא מנחה אותם לזוז הם מחליטים שזה הזמן ל:
אוקיי, אז מה כלכך מיוחד באלגוריתם? מה הוא מצליח לעשות עם הסקטורים האלה שאיכשהו גם עוזר לנו למנוע התנגשויות וגם עוזר לנו להיות יעילים? בואו תכירו את הקלאס שעושה את כל הקסמים: The Integrator (אנחנו פשוט נקרא לו המסנן מטעמי נוחות).
אז מה המטרה של המסנן? זוכרים שאמרנו שבכל משבצת שמורים שלושה שדות: מחיר, מחיר מסונן, ושדה זרימה? אז התפקיד של המסנן זה באמת לחשב את המחיר המסונן עבור כל משבצת רלוונטי.
בשונה מהמחיר הקבוע שיש לכל משבצת, המחיר המסונן הוא בעצם מחיר שלוקח בחשבון את היעד. "כמה שווה לך ללכת למשבצת הזאת, בהנחה שאתה רוצה להגיע ל- Goal?". השדה הזה יאפשר לנו בהמשך לחשב את השדה האחרון (הזרימה).
אז בואו נתחיל להבין איך המסנן עובד.
הדבר הראשון שהמסנן עושה, זה מגדיר שהמחיר המסונן של משבצת היעד הוא אפס. זה דיי הגיוני, הרי לא משנה מה, אם אנחנו ליד היעד אנחנו תמיד נרצה ללכת אליו.
עכשיו אנחנו נתחיל לחשב את שאר המחירים המסוננים, תוך כדי שאנחנו מתקדמים אחורה מהיעד שלנו. אתם יכולים לחשוב על זה קצת כמו על תנודות במים. אנחנו בעצם נוגעים ביעד, והתנודות שנוצרות "במים" הם המשבצות עבורן אנחנו מחשבים את המחיר המסונן. משהו כזה:

למי שסקרן: הגלים האלה מחושבים באמצעות Wave Propagation ובעזרת פונקציה שנקראת \(Eikonal\,\,equation\)
בתכלס, זה דיי מגניב ואינטואטיבי. כל כך מגניב ואינטואטיבי למעשה, שאנחנו חייבים לסבך את זה טיפה יותר. אל תתעצבנו עליי, זה למטרה טובה.
מה הבעיה אתם שואלים? תחשבו על זה ככה: אני יודע שעוד לא הגעתי לזה, אבל המחיר המסונן בסופו של דבר עומד להשפיע על זה שהחיילים ילכו תמיד באופן האופטימלי אל היעד. אם אנחנו פשוט נחשב מחיר מסונן לכל המשבצות הרלוונטיות, יקרה משהו לא יפה: כשהחיילים יתקרבו ליעד, במקום ללכת ישירות אליו, הם יתחילו לעשות "מיקרו תיקונים". תיקונים ממש קטנים במסלול שאכן כנראה יביאו אותם אליו יותר מהר, אבל טבעי זה לא יראה. אנחנו רוצים שכשהחיילים יכולים "לראות" את היעד, הם פשוט ילכו אליו.
אבל איך נעשה את זה? אז למעשה אני קצת הטעיתי אתכם. לפני שהמסנן עושה את הבדיקה עם הגלים, הוא קודם כל עושה בדיקת LOS – Line of sight. המסנן בעצם רוצה לדעת מאיזה משבצות אפשר כבר לראות את היעד? ואז מהמשבצות האלה החיילים כבר יכולים ללכת דוך ישר.
אני ממש רוצה להסביר כאן איך הבדיקה הזאת מתבצעת, אבל מרגיש לי שהפוסט הזה במילא ארוך מידי ועדיף פשוט להראות מה התוצאה שלה:

אוקיי. אז עכשיו אנחנו יודעים שחיילים על המשבצות האלה ירוצו ישירות אל היעד בקו ישר. מה עם שאר המשבצות?
עבורן המסנן עכשיו יחשב את המחיר המסונן.
זוכרים שאמרתי שהמחיר המסונן של היעד הוא 0? אז בשביל שיהיה קצת קל יותר להסביר את האלגוריתם, בואו נקבע שהמחיר המסונן של המשבצת האחרונה ממנה אנחנו מצליחים לראות את היעד הוא 0, ונתחיל משם. כלומר:

מעולה. עכשיו מה שנעשה זה בדיוק הגלים שהסברתי מקודם. אופן החישוב יהיה:
עבור כל משבצת, תוסיף את המחיר הקבוע שלה ואת המחיר המסונן הנמוך ביותר של אחד השכנים שלה.
בעצם אנחנו מתחילים ממשבצת האפס כלפי מעלה: עבור המשבצת הראשונה מעל משבצת האפס, נוסיף את המחיר שלה ועוד אפס. שכן השכן עם המחיר המסונן הנמוך ביותר הוא משבצת האפס. נמשיך לעשות את זה, עד שהשלמנו את כל הסקטורים הרלוונטים.
אז איך זה יראה אחרי השלב הזה? ככה:

"יותם. זה מספרים על משבצות. אתה כבר שעה חופר לי ועדיין לא ברור איך העיגולים אמורים להגיע ליעד."
נשבע לכם סיימנו.
עכשיו אנחנו רק צריכים לעבור על כל משבצת כזאת עם מספר, ולהגיד לה להצביע לשכן עם המספר הכי קטן. לא מאמינים לי שיש בזה היגיון? תסתכלו:

כל מה שעשיתי כאן, זה הפניתי כל משבצת לשכן עם המחיר המסונן הכי זול שלה. זה השדה האחרון שלנו: שדה הזרימה.
תדמיינו עכשיו שכל חייל לוקח צעד קדימה. שדה הזרימה יפנה אותם מאותו הרגע בקלות וביעילות לעבר המשבצת הראשונה ממנה הם יצליחו לראות את היעד שלהם.
לשיטה הזאת המון יתרונות. מעבר לכך שהיא מאפשרת לנו לצמצם התנגשויות, אנחנו יכולים גם לשמור יעדים ושדות זרימה שיצרנו לשימוש חוזר. ככה שאם מצבור יחידות מנסות עוד פעם להגיע ממקום דומה ליעד דומה, לא צריך לחשב הכל מחדש. רק הדבר הקטן הזה חוסך לנו כמויות עצומות של זמן CPU.
וזהו! אם הצלחתם להחזיק עד לפה, יש לכם את הערכתי האינסופית. מקווה שהצלחתי להנגיש את האלגוריתם, חשוב לדעת שעשיתי מעט קיצורים בהסבר, אבל האלגוריתם עובד באופן מאוד מאוד דומה לזה.
מוזמנים לשאול שאלות למטה 🙂
